Along axis variability Modelling the data Forward modelling in 2-dimensions

Constraints on the model

We ran a variety of models to test the limits that can be placed on the axial resistivity structure. Of particular interest are the constraints which can be placed on the mid-crustal low resistivity anomaly. The lowest reasonable resistivity for the anomalous body is 0.2 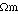, corresponding to pure basaltic melt at approximately 1300 ° C  (Waff & Weill, 1975). A melt lens of only 100 m thickness and a width of 4 km, consistent with the lens of very low velocity material detected seismically (Navin etal , this issue), cannot alone explain the data. Although there is a radial/azimuthal split for the data from Noddy, it is not as large as that observed in the data. The magnitude of the radial field enhancement caused by a low resistivity body increases quickly as the thickness of the body increases, levelling off for thicknesses greater than a skin depth (400 m in this case). Increasing the width of the melt lens up to 9 km improves the fit to the radial fields, but increasing the width past this results in a degradation of the fit to the azimuthal fields.

Although the data can be fit using a 400 m thick body of pure melt, such a large body of melt is incompatible with the seismic data, which suggest the presence of a much smaller melt lens, surrounded by a wider low velocity zone (Navin etal, this issue). Since there is a trade off between the size of the low resistivity zone and the resistivity within it, a body with a higher resistivity distributed over a wider region is also possible, and more likely given the seismic constraints. Instead of a thin body of very low resistivity, a thicker region with a higher resistivity can be used to explain the data so long as it is at least a skin depth thick. However, resistivities of 2.5 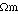or lower are required to reproduce the degree of splitting between the radial and azimuthal fields which is observed, requiring a thickness of at least 1300 m. The maximum thickness of the low resistivity anomaly cannot be constrained with the CSEM data, although the MT results (Heinson etal, this issue) are best fit when the low axial conductance is confined to the upper 3 km of the crust.

The fit of the response is not adversely affected by varying the depth to the top of the low resistivity anomaly between 1.8 km and 2.5 km below the seafloor. Increasing the depth past 2.5 km results in a significant decrease in the 0.75 Hz response between 5 km and 9 km source receiver range. When the top of the anomaly is shallower than 1.8 km, the low resistivity zone severely attenuates fields diffusing through the axis. In this case the response in the range 9-15 km, corresponding to the data recorded by Noddy, severely underestimates the observed amplitudes. The best results are obtained when the wi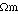dth of the 2.5 region is in the range 7-9 km. If the region is too narrow there is insufficient enhancement to explain the magnitude of the predominantly radial Quail tow 2 and Noddy tow 1 data. Increasing the width of the 2.5 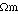 region too far results in response amplitudes which overestimate the magnitude of the Noddy data from the second source tow.

The minimum width of the structure above the low resistivity anomaly is constrained by the short range data from Quail. The 11 Hz data in particular can be adequately fit with a 1-dimensional resistivity structure, implying that they are not affected by lateral changes in resistivity. In order for the 11 Hz data to be unaffected by the increase in resistivity with distance from the axis, the width of the axial region above the mid-crustal anomaly must be greater than 2 km. Constraint on the maximum width of the structure above the anomaly comes from examining the off axis ELF data. Increasing the width of the shallow axial structure results in an increase in attenuation of fields diffusing through the axis. Since the fields detected by the ELF instruments have all diffused through the axial zone, this results in a decrease in all amplitudes. Similarly decreasing the width results in an increase in the amplitudes. However, a decrease in attenuation will increase the azimuthal fields more than the radial fields, reducing the split between the two components. A balance must therefore be found between the width of the shallow axial structure, which controls the overall level of the response, and the magnitude of the sub-axial anomaly, which controls the splitting between the radial and azimuthal components. The resistivity of the mid-crustal anomalous region in Figure. 7 is chosen to be as as high as possible while still reproducing the features observed in the data. For this anomaly, the width of the shallow low resistivity on axis is fairly well constrained at 4-5 km.

Along axis variability Modelling the data Forward modelling in 2-dimensions

Go to first page