Constraints on the model Modelling the data Inversion of the data

Forward modelling in 2-dimensions

We have undertaken further and more detailed analysis of the CSEM data using finite element modelling based on the assumption that the resistivity structure is 2-dimensional, with an axis of symmetry parallel to the trend of the AVR. The 1-dimensional inversion results suggest that the dataset cannot be simultaneously satisfied by a 1-dimensional model, while all viable geodynamic models of mid-ocean ridge systems indicate that we should expect large variations in structure to occur in a plane parallel to the spreading direction. Although the extent to which along axis as well as across axis variations in structure are important at ridges remains to some extent unresolved, a 2-dimensional approach as a first approximation is justified by two factors. Firstly all of our data come from within one spreading segment, as defined by the AVR. Secondly data collected on Quail during the first source tow show no variation between the signals detected when DASI was to the north and those when DASI was to the south of the instrument suggesting that, in the vicinity of this instrument at least, there is along axis uniformity. We will return to the question of possible along axis variations in the deeper crustal structure in a later section.

In the 2.5-dimensional finite element modelling code of Unsworth (1991), the 2-dimensional region of interest is discretised into area elements each associated with a number of nodes. The solution for the electromagnetic fields is approximated by the values at the nodes, and within each area is linearly interpolated using a series of basis functions. Unsworth (1991) examined the effect of seafloor topography of the type which is encountered at fast spreading mid-ocean ridges such as the East Pacific Rise. The seafloor was allowed to slope away from the axis at angles of between 2.5° and 10° . The seafloor topography at the Reykjanes Ridge (Figure. 7a,b) is more complicated than the rather subdued topography of the East Pacific Rise. The effect of this rugged topography on the response must therefore be included in the modelling.

The resistivity structure is defined at the mesh generation stage, by assigning a resistivity to each rectangular region within a rectilinear mesh. These regions are then subdivided into triangular elements by the mesh generator itself. Using a structure definition of this sort, sloping seafloor topography can only be modelled as a series of small steps within the rectilinear mesh. This is both inaccurate and unrealistic. Wannamaker etal (1986) studied the effect of 2-dimensional topography on MT data, and solved this problem by making the earth-air interface follow the sides of triangular elements within a finite element mesh.

Here the problem is solved by distorting a rectilinear mesh to follow a specified seafloor topography. An upper and lower level, and are defined, between which the mesh is distorted. The position of the row of seafloor nodes, , is also specified. New node positions are calculated so that

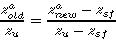
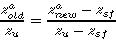
for rows of nodes above the seafloor, and

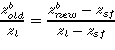
for rows of nodes below the seafloor, where and refer to an undistorted part of the mesh. There must be enough rows of nodes between and to ensure that when the mesh is stretched, as it would be under a hill, the vertical mesh spacing does not become too wide to accurately represent the fields. Model parameterisations including topography are therefore extremely computationally expensive, especially for models containing low resistivity regions. Because of this, it proved impossible to model 11 Hz data with the bathymetry included. A flat seafloor approximation was therefore used to explore, by forward modelling, large regions of model space. Topography was then included during the final stages of modelling to refine and validate the conclusions.

Shown in Figure. 7 is the real bathymetry along a line perpendicular to the AVR axis and passing through its centre and the final model of ridge resistivity structure and topography. The response, which fits the data to RMS 2.3, is plotted in Figure. 7 (d). The resistivity structure to a depth of 1 km on the axis of the AVR is constrained by the on axis data recorded by Quail during the first tow. Below this the resistivity must be increased to fit the off axis data (the 40 region in the model). The resistivity outside the axial region is not well constrained by the data and is therefore chosen to be broadly consistent with the results of previous CSEM experiments (Young & Cox, 1981; Cox etal , 1986; Evans etal, 1994; Constable & Cox, 1996) and the borehole measurements of Becker (1985). However, a simple increase in crustal resistivity with distance from the AVR axis cannot explain the data. The dashed line in Figure. 7 (d) shows the response of the model in (c) with the 1lens and surrounding 2.5region removed. Although the amplitudes of the data are of the right order, the large split between the predominantly radial Noddy tow 1 and predominantly azimuthal Noddy tow 2 data is not reproduced. Sinha etal (1997) demonstrated that when the seafloor is flat, a zone of low resistivity must be included beneath the axis to explain this feature of the data. Here we show that this conclusion is not altered by the inclusion of realistic seafloor topography.

The resistivity of the mid-crustal low resistivity anomaly is chosen to be as high as possible while still reproducing the features seen in the data with some degree of accuracy. A 100 m thick, 4 km wide lens of melt is included at a depth of 2.1 km below the axis. This has a resistivity of 1 , a value near the upper end of possible resistivities of a pure basaltic melt (Waff & Weill, 1975). Although this lens has a small effect on the response, it cannot be constrained independently of the surrounding 2.5 region, and is included only for consistency with the structure detected by the seismic experiment (Navin etal, this issue). The splitting effect between the radial and azimuthal fields is governed by the 2.5 region. Increasing the resistivity of this region decreases the degree of enhancement of the radial fields, and consequently degrades the fit of the model. The dimensions of this low resistivity anomaly are compatible with the constraints placed on the size of the low resistivity anomaly by the CSEM data. However the exact shape of the region is not constrained by the CSEM data. Since the seismic data have a greater structural resolution than the diffusive electromagnetic fields, the shape of the 2.5 region is chosen to be coincident with the region in which the P-wave velocity anomaly is greater than -0.4 km/s (Navin etal, this issue). However, there is little difference in the response between the anomaly shown in Figure. 7 and a simple rectangular anomaly which also satisfies the constraints on dimension discussed in the next section.

The seafloor topography produces a small downward shift in 0.35 Hz and 0.75 Hz amplitudes, but the character of the response is governed by the crustal resistivity structure, and therefore the main conclusions of the modelling with a flat seafloor are valid. For this experiment the effect of the rugged seafloor topography is to increase the need for a region of low resistivity below the axis. A resistivity of 2.5 should therefore be regarded as the highest resistivity in the mid-crustal anomaly which is capable of producing the required split between the azimuthal and radial data.

The main area of misfit is in the on axis 0.35 Hz data recorded by Quail during the first tow. The data can be fit, however, if the seafloor topography appropriate to this instrument is used. Shown in Figure. 7 (a) is a bathymetric profile along a line perpendicular to the AVR axis and passing through the position of instrument Quail. The on axis response at 0.35 Hz of the model with this more northerly topography represented is plotted in Figure. 7(d). Although computer memory limitations prevented modelling of the high frequency data using a distorted mesh, results using models in which the topography of the AVR was represented by a simple elevated block suggest that the effect of the topography on the 11 Hz data would be minimal. In order to simultaneously satisfy the entire dataset, topography varying in 3-dimensional would be required.

Constraints on the model Modelling the data Inversion of the data

Go to first page