Forward modelling in 2-dimensions Modelling the data Modelling the data

Inversion of the data in 1-dimension

Data will be divided into two subsets (Figure 3); on axis data consisting of 0.35 Hz and 11 Hz signals detected by Quail during tow 1, covering source-receiver offsets of 1-5 km; and off axis data, collected with the source, receiver or both away from the AVR crest, covering source-receiver ranges of 3-15 km and consisting of signals recorded by ELF Noddy during tow 1 and Quail, Noddy and Kermit during tow 2.

On axis data. The Occam inversion process requires an a priori estimate of the data error, but quantifying these errors can be difficult. Although geometric errors associated with the source-receiver position and geometry can be estimated, scatter in the data caused by small scale heterogeneity in the crust over which the source is moving is much harder to quantify (Evans etal , 1994; Unsworth, 1994). We used a method of determining the appropriate level of misfit by successively reducing the required tolerance until the structure is removed from the residuals, as described in Constable & Cox (1996).

The variation of the model resulting from joint inversion of the 0.35 Hz and 11 Hz data as the misfit is reduced is illustrated in Figure. 4. It can be seen that as the misfit decreases, the largest variations in the model are at depths greater than around 1 km. Shallower than this, the resistivity contours are nearly parallel to the misfit axis, implying that in this region the resistivity structure is well constrained and the steep resistivity gradient is required. Below 1 km there is less constraint, so the variation in misfit is accommodated by resistivity variations in this region. The effect of over-fitting the model is clear. The resistivity contours bend back on themselves at very low misfit, evidence of the rough and oscillatory structures that are produced.

The vertical dashed line in Figure. 4 marks the level of misfit deemed appropriate on the basis of the structure in the residuals. The corresponding model is plotted in Figure. 5 along with its response, which fits to RMS 1.3. The CSEM method by itself cannot resolve sharp resistivity discontinuities, and the Occam inversion models any such discontinuities as a rapid but smooth variation in resistivity. However, the seismic model of the upper crust (Navin etal, this issue) features steep velocity gradients but no discontinuities, suggesting that the smooth electrical model is reasonable. The response of the model fits the 11 Hz data and the shortest range 0.35 Hz data well, but there is a small bias in the fit to the longer range 0.35 Hz data. We show later that this mismatch can be reconciled if the seafloor topography around Quail is included. The resistivity in the upper 10-100 m of the model is much lower than that of seawater, and is likely to be the result of the 1-dimensional inversion trying to fit the effect of the known 2-dimensional seafloor topography. The 11 Hz data are much less affected by topographic effects than the 0.35 Hz data, because the skin depth at 11 Hz is much shorter so the induction is more local. The model resulting from inversion of the 11Hz data alone to RMS 1.5 (Figure. 5) therefore gives a better estimate of the shallow resistivity beneath Quail.

Also shown in Figure. 5 is the model resulting from 1-dimensional inversion of the on axis transverse electric (TE) mode MT data to RMS 1.5 (Heinson , this issue). In the upper 1 km of the structure the CSEM and MT models do not differ greatly, and the MT model fits the on axis CSEM data to RMS 1.55. Although the consistency between the two independent electromagnetic techniques is impressive, it should be noted that in both cases the subset of the data which is most likely to be 1-dimensional has been inverted. Higher dimensional structure is required to satisfy the complete MT and CSEM datasets, however the agreement between the CSEM and MT results persists (Heinson etal , this issue).

Off axis data. The noticeable feature of the off axis data (Figure. 3) is the large difference in amplitude between the 0.75 Hz data recorded on Noddy during tow 2 and the 0.35 Hz data recorded by the same instrument during tow 1. It can be seen in Figure. 7 that difference in frequency has only a small effect on the response, however there is a pronounced difference in source receiver geometry: during tow 1, Noddy was along strike from the source so the fields detected were predominantly radial (parallel to the line joining the source and receiver). During tow 2 the source was on the opposite side of the AVR axis from the instrument so the fields detected were predominantly azimuthal (perpendicular to the line joining the source and receiver). One would expect some level of anisotropy caused by ridge parallel cracks and fissures, but the results of Yu & Edwards (1992) suggest that because the transmitter is always parallel to the strike of the AVR, the effect of any anisotropic structure would have been similar throughout the experiment.

The large difference in amplitude between these two groups of data can be explained by the geometrical effect on the response of buried conductive layers. The magnitude of the radial fields is enhanced by the presence of conductive layers, an effect described in terms of galvanic current channelling by Unsworth (1991) or a lithospheric waveguide by Chave etal (1990). In contrast, azimuthal fields are more strongly affected by the attenuative effects of a conductive layer. If there is any increase in the field magnitude, it is much less than that observed in the radial component. This results in a distinctive radial/azimuthal field split. Inverting the off axis ELF data to RMS 2.2 produces the model shown in Figure. 6. There is a significant positive bias in the residuals, especially those associated with the Noddy tow 1 and Quail tow 2 data points but attempting to reduce the misfit further leads to divergence problems in the inversion without improving the fit to the data. As expected, the model features a downturn in resistivity at a depth of 1-5 km. The lack of off axis short range data means that structure much shallower than this is poorly resolved, but resistivities are considerably higher than in the on axis model (85 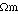 vs 10 ).

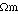Forward modelling in 2-dimensions Modelling the data Modelling the data

Go to first page